===============================
학습내용
[Graph 9강] 그래프 신경망이란 무엇일까? (기본)
정점 표현 학습의 목적은 이것.
전 강의에선 변환식 임베딩 방법을 썼지만 한계가 있어서 귀납식 방법을 쓴다. 즉 벡터를 넣고 벡터를 반환받는게 아니라 모델 자체(인코더)를 반환 받는다.
대표적 귀납식 임베딩 방법인 그래프 신경망(Graph Neural Network)를 사용할 것.
그래프 신경망 기본
그래프의 인접행렬을 A라고 하면 A의 크기는 |V| *|V| 가 된다.
각 정점 u의 속성(Attribute) 벡터를 Xu 라고 하고, 정점 속성 벡터 Xu는 m차원 벡터고, m은 속성의 수로 하자.
그럼 각 정점들을 임베딩 했으니 각 층에 넣어서 학습할 수 있다. 이웃들을 다같이 입력값으로 넣어 계산하는 방식이라 구하고자 하는 대상 정점에 따라 구조가 달라질 수 있다.
각 층에 대한 학습 변수는 같다. 즉 Weight가 같다는 말.
그럼 입력값이 매번 달라지는데 어떻게 입력을 하냐? 그래서 이웃 정보들의 평균을 계산하고 신경망에 넣는다.
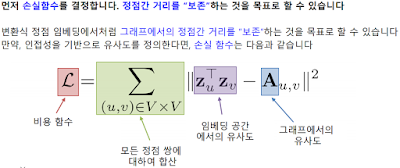
그래서 위 식처럼 hidden vector를 정의한다. W와 B는 각 층 k마다 다르고, 학습되는 환경변수다. Loss function도 임베딩에서의 공간유사도와 그래프에서의 유사도가 일치하게 끔 학습하도록 정의한다. 원래 목적이 그거였으니까.
또 후속과제라고 목적 자체가 해당 정점에 대해 파악하는 것도 있을 수 있다. 이런 경우는 후속 과제(Downstream Task)의 손실함수를 이용한 종단종(End-to-End) 학습도 가능하다고 한다. 이 목적에 맞춰서 loss function을 달리 정의하는 듯.
보면 왠지 CNN 과 비슷하게 생겼는데 실습할 때도 비슷한 방식으로 넣더라. 이렇게 End-to-End로 학습하는게 성능도 잘 나온다 하더라.
이런 귀납식 방법을 썼기 때문에, 변환식이 못한 것을 해낸다.
그래프 신경망 변형
위에서 한건 그래프 신경망의 기본 형태였고, 이 신경망을 다양하게 개조해서 사용한다고 한다. 다양한 형태의 집계 함수를 사용한다고 한다.
그래프 합성곱 신경망(Graph Convolution Network, GCN)의 집계 함수. Bk를 Wk에 하나로 퉁쳤다.
Graph SAGE의 집계 함수. GCN처럼 Bk를 Wk로 퉁치는건 걱정이 되었는지 concat으로 그냥 벡터의 길이를 늘려 추가하는 방식으로 했다. AGG 함수로 약간 일반화 시켜 목적이나 원하는 함수를 넣을 수 있게 한 것 같다.
합성곱 신경망(CNN)과 비교
둘다 이웃의 것을 사용하기 때문에 비슷하다고 볼 수 있으므로 그냥 기존에 만든 CNN에 넣으면 되는거 아니냐 라고 생각할 수 있다. 하지만 입력되는 수가 다르기도 하고, 제일 큰 이유는 바로 옆에 있는 이웃과 정보가 연관되어 있지 않기 때문에 사용할 수 없다.
실습
https://colab.research.google.com/drive/1_HT5Dy7YQ4b2601GhLC4PzlN2TxdUbks?usp=sharing
[Graph 10강] 그래프 신경망이란 무엇일까? (심화)
그래프 신경망에서의 어텐션
위에서 한 것도 한계가 있다. 각 이웃들마다 가중치를 부여하지 않았기 때문에 제성능을 잴 수 없단 것.
그래서 각 이웃들 마다도 가중치를 적용한다. 진짜 가중치 엄청 좋아한다. 각 이웃들마다 어디에 집중할지 다른 가중치를 부여하기 때문에 어텐션이라고 부르는 것 같다.
이 가중치를 얼마나 부여할지도 학습한다. 그래서 학습변수가 W, aT 가 된다.
그래프 신경망은 언제 사용되는가
1) 개별 정점의 임베딩을 얻을 때 2) 군집 구조로 묶어줄 때(군집을 찾는데) 3) 이것들을 군집 내에서 합산할 때 즉 합산하는 방법 자체 총 3종류의 곳에서 그래프 신경망이 활용되고 있다.
여러개를 동시에 학습할 수 있다고 한다. 행렬 곱 특성 때문인가? 가능하다는데 뭐
어쨋든 이렇게 하면 성능이 좀더 잘 나온다.
그래프 표현 학습과 그래프 풀링
그래프 자체를 임베딩을 하는 것.
그래프 풀링(Graph Pooling)이란 정점 임베딩들로부터 그래프 임베딩을 얻는 과정입니다
평균 등 단순한 방법보다 그래프의 구조를 고려한 방법을 사용할 경우 그래프 분류 등의 후속 과제에서 더 높은 성능을 얻는 것으로 알려져 있습니다.
아래 그림의 미분가능한 풀링(Differentiable Pooling, DiffPool)은 군집 구조를 활용 임베딩을 계층적으로 집계합니다.
화학분자 구조모형 분석 같이 그래프 자체가 의미가 있을 때 하는 것 같다.
지나친 획일화 문제
레이어 크기를 늘릴수록 다른것들끼리 유사하다고 판단해서 구별이 안된다. 이게 무슨 말이냐면 레이어를 늘리면 간선이 저 멀리까지 가서 해당 정점이 아주 멀리있는 다른 정점들까지 고려해서 파악이 되다보니 서로 다른게 아니라고 학습이 되는거. 그래서 레이어가 커질수록 서로 관련이 깊어지고, 그러다보니 임베딩이 비슷해진다.
실제로 그래프 그려보면 레이어가 많을 수록 성능이 떨어진다.
그래서 APPNP의 경우 0번째 레이어를 제외하고 모든 층의 임베딩을 함께 사용한다고 한다. 단순하게 집계해서 어떻게 처리하는것 같다. 몰라 여기 이해 안가니까 나중에 찾아봐야 한다.
그래서 저 방법을 쓰니까 레이서 수가 많아도 상관없더라. 라는 결론이 나온다.
그래프 데이터의 증강
임의 보행을 먼저 수행해서 유사도가 높은 정점 간에 간선을 추가해서 데이터 증강을 한다고 한다. 그러니가 원래 입력 그래프에서도 데이터가 누락되거나 부정확한 간선이 있을 수 있기 때문에 얘는 분명이 간선이 있을텐데 없다면 그걸 이어주고 학습하는 것이다. 그럼 더 정확한 학습이 된다는 생각. 실제로 개선된다고 한다.
실습
https://colab.research.google.com/drive/1vyWTB9gnrWlch3jgmq_4K4RDWhmt1jQr?usp=sharing
================================
피어세션
end to end는 노드 임베딩보다는 목적이 원래 그 노드에 대한 classification 하는 거니까 그거에 맞춰서 한 거인듯.
결합한다. 그래서 이름이 GraphSAGE라는 라이브러리 이름을 가지는 듯.
GNN 여기가 설명 더 쉽게 하는 것 같다: https://www.youtube.com/watch?t=2229&v=NSjpECvEf0Y&feature=youtu.be
SK는 양식주는데 맞춰서 하면 된다. 코테가 1문제가 진짜 어려웠다.
CNC는 인성 보는 듯. 햇으면 뭐.. 적으면 되겠지.
면접볼때 약간 보수적인 기업들 (은행 등 금융권) 같은 경우는 정장을 입어야 하고 IT나 다른 개방적인 곳은 안해도 됨. 아얘 금지하는 곳도 있다.
===========================
마스터 세션
지금은 추천시스템 수요가 많이 없지만 그만큼 공급은 더 없어서 취업에 유리할 거라고 생각.. 사실 잘 모르겠다.
데이터셋들
https://ogb.stanford.edu/
http://web.stanford.edu/class/cs224w/
그 외 kaggle 등에도 추천시스템 하면 관련 대회 많이 나온다.
책
Networks, Crowds, and Markets
추천논문 ( 단하나만 한다면.ㅏ.)
https://arxiv.org/abs/1303.4402
=================================
후기
공부하기가 싫어짐.
근데 내 길은 추천 시스템이 될 것 같다. 일단 주말이니까 좀 놀다가 하고싶을때 하자.
